অধ্যায় ১০মঃ জ্যামিতি

অধ্যায় ১০মঃ জ্যামিতি| তৃতীয় শ্রেণি গণিত বই সম্পূর্ণ সমাধান | Class Three (03) Math Book Solution | Chapter Ten (10) – Geometry

তৃতীয় শ্রেণির গণিত অধ্যায় ১০ জ্যামিতির , নিজে কর অংশের উত্তরের সাথে সাথে অতিরিক্ত সংক্ষিপ্ত ও সৃজনশীল অংশের উত্তর দেওয়া রয়েছে।

জ্যামিতি

এই অধ্যায়ের গুরুত্বপূর্ণ তথ্যসমূহ

⇒ তলঃ একটি ঘনের বাইরের অংশকে তল বলে।

⇒ প্রত্যেক তলে অসংখ্য বিন্দু আছে।
⇒ প্রত্যেক তলে অসংখ্য রেখা আঁকা যায়।
⇒ প্রত্যেক রেখায় অসংখ্য বিন্দু আছে।
⇒ রেখা সরল বা বক্র হতে পারে। বৃত্ত একটি বক্র রেখা।
⇒ এক বিন্দুতে মিলিত হলে একটি কোণ তৈরি হয়।
⇒ চতুর্ভুজের চারটি বাহু আছে।
⇒ চতুর্ভুজের চারটি কোণ আছে।
⇒ আয়তের বিপরীত বাহুগুলোর দৈর্ঘ্য একই।
⇒ বর্গের চারটি বাহুর দৈর্ঘ্য একই।

জ্যামিতি : ‘জ্যা’ অর্থ ভ‚মি এবং ‘মিতি’ শব্দের অর্থ হলো পরিমাপ। সুতরাং জ্যামিতি শব্দের অর্থ হলো ভ‚মির পরিমাপ। গণিতের যে শাখায় ভ‚মির পরিমাপ, আকার ও আকৃতি সম্পর্কে আলোচনা করা হয়। তাকে জ্যামিতি বলে।
জ্যামিতি শাস্ত্র অধ্যয়ন করার জন্য প্রাথমিক কিছু বিষয় জানা খুবই গুরুত্বপূর্ণ। এগুলো হলো বিন্দু, রেখা, তল, কোণ, ত্রিভুজ ও চতুর্ভুজ।
বিন্দু : যার দৈর্ঘ্য, প্রস্থ ও বেধ নেই, শুধু অবস্থান আছে, তাকে বিন্দু বলে।

এখানে, ক একটি বিন্দু।
রেখা : যার দৈর্ঘ্য আছে, প্রস্থ বা উচ্চতা কিছুই নেই, তাকে রেখা বলে। যেমন-

চিত্রে কখ একটি রেখা।
কোণ : দুইটি রেখার মিলিত বিন্দু (শীর্ষবিন্দু) থেকে যে আকৃতি তৈরি হয়, তাকে কোণ বলে।

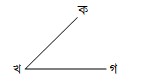
চিত্রে, ∠কখগ একটি কোণ। কোণ বুঝাতে ‘∠’ চিহ্ন ব্যবহৃত হয়।
কোণ তিন প্রকার।

১। সমকোণ : যে কোণের পরিমাণ ৯০° (ডিগ্রি) তাকে সমকোণ বলে। এখানে নব্বইয়ের উপর ‘^০’ চিহ্ন দ্বারা ডিগ্রি বোঝানো হয়।

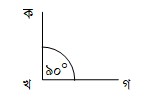
চিত্রে, ∠কখগ একটি সমকোণ।
২। সূক্ষ্মকোণ : যে কোণ এক সমকোণ বা ৯০° অপেক্ষা ছোট তাকে সূ²কোণ বলে।

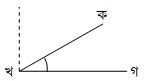
চিত্রে, ∠কখগ একটি সূ²কোণ।
৩। স্থুলকোণ : যে কোণ এক সমকোণ বা ৯০° অপেক্ষা বড় তাকে স্থুলকোণ বলে।

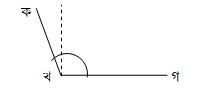
চিত্রে, ∠কখগ একটি স্থুলকোণ।
চতুর্ভুজ : চারটি ভুজ বা বাহু দ্বারা আবদ্ধ আকৃতিই হল চতুর্ভুজ।

চিত্রে, কখগঘ একটি চতুর্ভুজ।
আয়ত : যে চতুর্ভুজের চারটি কোণই সমকোন এবং বিপরীত বাহুগুলোর দৈর্ঘ্য একই, তাকে আয়ত বলে।

dfdsgdgfg

চিত্রে, বিপরীত বাহু দুইটির দৈর্ঘ্য সমান ও ৪টি কোণ সমকোণ বা ৯০°।
বর্গ : যে চতুর্ভুজের ৪ কোন সমকোন ও ৪ বাহুর দৈর্ঘ্য সমান তাকে বর্গ বলে।

চিত্রে, ১, ২, ৩ ও ৪ নং সবগুলো বাহুর অর্থাৎ চারটি বাহুর দৈর্ঘ্য একই এবং চারটি কোণের প্রত্যেকটি সমকোণ বা ৯০°।
বৃত্ত : বৃত্ত একটি বক্ররেখা। বিভিন্নভাবে বৃত্ত অঙ্কন করা যায়। যেমন- চুড়ির সাহয্যে, সুতা ও পেনসিলের সাহায্যে, গøাস ব্যবহার করে, কৌটার মুখ ইত্যাদি ব্যবহার করে বৃত্ত অঙ্কন করা যায়।

চিত্রে, কখগ, রৈখিক গতিপথ হলো বৃত্ত।

১০ নিজে করি: প্রশ্ন ও উত্তর

১। বিভিন্ন ধরনের গোলাকার বস্তু ব্যবহার করে বৃত্ত আঁকি।

এক তা কাগজের ওপর একটি চুড়ি রাখি। চুড়ির চারদিকে দাগ টানি। এতে একটি বৃত্ত আঁকা হলো।
এভাবে কাগজের উপর যেকোনো গোলাকার বস্তু (যেমন- গøাসের মুখ, কৌটার মুখ, কয়েন ইত্যাদি) রেখে চারপাশে দাগ টেনে বৃত্ত আঁকা যাবে।

২। সুতা ও পেনসিল ব্যবহার করে বৃত্ত আঁকি।

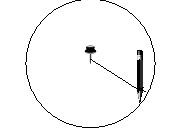
একটি কাগজে উপর বোর্ড পিন আটকাই এবং বোর্ড পিনের সাথে সুতা দিয়ে বাঁধি। সুতার অপর প্রান্তে পেনসিল বাঁধি। এখন বোর্ড পিনের চারদিকে সুতা টানটান রেখে পেনসিল ঘুরিয়ে দাগ টানি। এতে একটি বৃত্ত আঁকা হলো।

৩। তুমি একটি বৃত্ত আঁকার পর, বৃত্তটি কাট এবং কীভাবে বৃত্তটির কেন্দ্র বের করা যায় তা চিন্তা কর। (তুমি বৃত্তটি ভাঁজ করে অর্ধেক কর এবং …)

আমি একটি সাদা কাগজের উপর চুড়ি স্থাপন করে এর চারদিকে রেখা টানলাম। ফলে কাগজটিতে নিচের মতো একটি বৃত্ত অঙ্কিত হলো।

আমি কাগজ থেকে বৃত্তের অংশ কাটলাম। ফলে নিচের বৃত্তটি পেলাম।

উপরের কর্তিত বৃত্তের অংশটিকে নিচের মতো ভাঁজ করে অর্ধেক করি।

এক্ষেত্রে প্রথমে কাটা বৃত্তটিকে ভাঁজ করে অর্ধেক করি। অর্ধবৃত্তটি আবারও ভাঁজ করে অর্ধেক করি। এবার ভাঁজগুলো খুলে বৃত্তের আগের অবস্থায় নিয়ে এসে পর্যবেক্ষণ করি। দেখা যাবে যে বৃত্তটিতে দুইটি সরলরেখা ভাঁজ হওয়া অংশগুলো প্রকাশ করেছে। রেখা দুইটি পরস্পর একটি বিন্দুতে ছেদ করেছে। এই ছেদ বিন্দুই হলো বৃত্তের কেন্দ্র।

ব্যাখ্যা ও সমাধানঃ প্রথমে বৃত্তটি ভাজ করে অর্ধেক করি। অর্ধেক করার পর তাকে আবার ভাজ করে চার ভাগের এক ভাগ করে ফেলি। এবার কাগজ মেলে দেখি দুটি কাগজের ভাজ (বেখার ন্যায়) মাঝখানে একটা ছেদ বিন্দু তৈরি করেছে। এটাই বৃত্তটির কেন্দ্র।

৪। একটি বৃত্ত অঙ্কন কর। বৃত্তটি ভাঁজ কর। এখন ভাব, কীভাবে বৃত্তটির কেন্দ্র খুঁজে বের করা যায়।

৩ নং প্রশ্নের সমাধান থেকে বৃত্তটি আঁক।
বৃত্তের কেন্দ্র খুঁজে বের করার প্রক্রিয়া :
এক্ষেত্রে ছিদ্র করার জন্য আলপিন ব্যবহার হবে।

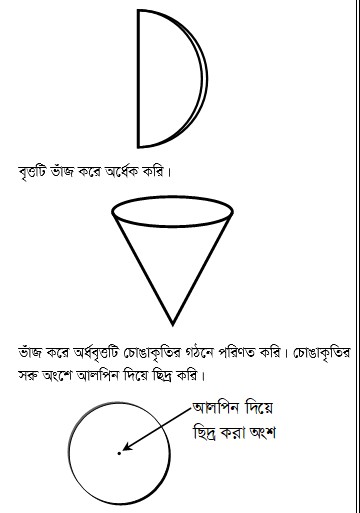
আলপিন দিয়ে ছিদ্র করা অংশটিই বৃত্তের কেন্দ্র। এভাবেই বৃত্তটির কেন্দ্র খুঁজে বের করা যায়।

তৃতীয় শ্রেণির গণিত অধ্যায় ১০ জ্যামিতি সংক্ষিপ্ত প্রশ্নের উত্তর

■ সাধারণ
১. বৃত্ত কী?
উত্তর : বৃত্ত একটি বক্ররেখা।
২. বর্গ কী?
উত্তর : যে চতুর্ভুজের চারটি বাহুই সমান এবং সব কোণ ৯০° তাকে বর্গ বলে।
৩. আয়ত কী?
উত্তর : যে চতুর্ভুজের বিপরীত বাহগুলো সমান এবং সবগুলো কোণ ৯০°, তাকে আয়ত বলে।
৪. জ্যামিতি বলতে কী বোঝায়?
উত্তর : জ্যামিতি বলতে ভ‚মির পরিমাপকে বোঝায়। জ্যা অর্থ ভ‚মি, মিতি অর্থ পরিমাপকে বোঝায়।
৫. ফুটবলের উপরিভাগকে কী তল বলে?
উত্তর : ফুটবলের উপরিভাগকে বক্রতল বলে।
৬. কাগজের উপরিভাগ কী?
উত্তর : কাগজের উপরিভাগ একটি তল।
৭. কোণ কয় প্রকার?
উত্তর : কোণ ৩ প্রকার।
৮. চিত্রটি কীসের?
উত্তর : আয়তের।
৯. চিত্রটি কীসের?
উত্তর : বর্গের।
১০. নিচের চিত্রটি কোন ধরনের তলের?

উত্তর : সমতল।
১১. নিচের চিত্রটির নাম কী?

উত্তর : বৃত্ত।
 যোগ্যতাভিত্তিক
১২. ২ সমকোণ সমান কত ডিগ্রি?
উত্তর : ১৮০০।
১৩. , চিত্রের কোণটির নাম কী?
উত্তর : স্থূলকোণ।
১৪. একটি বইয়ের উপরিভাগকে কী বলে?
উত্তর : একটি বইয়ের উপরিভাগকে তল বলে।

তৃতীয় শ্রেণির গণিত অধ্যায় ১০ জ্যামিতি কাঠামোবদ্ধ প্রশ্নের উত্তর (যোগ্যতাভিত্তিক)

১। চিত্রগুলো লক্ষ কর ও প্রশ্নগুলোর উত্তর দাও :

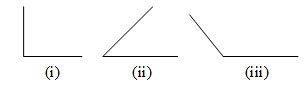
ক. (র) নং চিত্রটির নাম কী এবং এটি কত ডিগ্রির সমান? ২
খ. (রর) নং চিত্রটির কোণের নাম এবং কোণের পরিমাপ কত পর্যন্ত হয়? লেখ। ২
গ. (ররর) নং চিত্রটির কোণের নাম এবং কোণের পরিমাপ কত পর্যন্ত হয়? লেখ। ২
ঘ. কোণ কীভাবে তৈরি হয়? ২
ঙ. (ররর) নং চিত্রটির কোণের সংজ্ঞা দাও। ২

সমাধানঃ

ক. (র) নং চিত্রটির নাম সমকোণ। এটি ৯০° সমান।
খ. (রর) চিত্রটির নাম সূক্ষ্ণকোণ এবং কোণ ৯০^০ অপেক্ষা ছোট।
গ. (ররর) নং চিত্রটির নাম স্থুলকোণ এবং কোণ ৯০^০ অপেক্ষা বড় কিন্তু ১৮০০ অপেক্ষা ছোট।
ঘ. দুইটি রেখার মিলিত বিন্দুতে একটি কোণ তৈরি হয়।
ঙ. (ররর) নং চিত্রটি স্থুলকোণ। সমকোণের চেয়ে বড় কোণকে স্থূলকোণ বলে।

২। চিত্রগুলো লক্ষ কর ও প্রশ্নগুলোর উত্তর দাও :

ক. (র) নং চিত্রটিতে চতুর্ভুজটির নাম কী? ২
খ. (রর) নং চিত্রটিতে চতুর্ভুজটির নাম কী? ২
গ. (র) নং চিত্রে বিপরীত বাহুগুলো কী রকম? ২
ঘ. (রর) নং চিত্রে বাহুগুলো কী রকম? ২
ঙ. (র) ও (রর) নং চিত্রে প্রত্যেকটি কোণের নাম কী? ২

ক. (র) নং চিত্রে চতুভুর্জটির নাম আয়ত।
খ. (রর) নং চিত্রে চতুর্ভুজটির নাম বর্গ।
গ. (র) নং চিত্রে বিপরীত বাহুগুলো পরস্পর সমান।
ঘ. (রর) নং চিত্রে বর্গের প্রত্যেকটি বাহু সমান।
ঙ. (র) ও (রর) নং চিত্রে প্রত্যেকটি কোণের নাম সমকোণ।

এই ক্লাসের অন্যান্য অধ্যায়ের সমাধান দেখুন