১০ম অধ্যায়ঃ বৃত্ত | ৮ম শ্রেণি গণিত বই সম্পূর্ণ সমাধান | Class Eight (08) Math Book Solution | Chapter 10 : Circle| Class 8 math book Online Solution in Bangla (BD)
১০ম অধ্যায়ঃ বৃত্ত | অনুশীলনী ১০.২ : বৃত্তের উপপাদ্য: জ্যা সম্পর্কিত – PDF
১০ম অধ্যায়ঃ বৃত্ত | অনুশীলনী ১০.২ এর সকল প্রশ্ন ও উত্তর এখানে রয়েছে। ৮ম শ্রেণি সম্পূর্ণ গণিত বই সমাধান
৮ম শ্রেণির গণিত ১০ম অধ্যায় অনুশীলনী ১০.২ প্রশ্ন ও সমাধান
১. বৃত্তের দুইটি সমান জ্যা পরস্পরকে ছেদ করলে দেখাও যে, এদের একটির অংশদ্বয় অপরটির অংশদ্বয়ের সমান।
সমাধানঃ
বিশেষ নির্বচনঃ
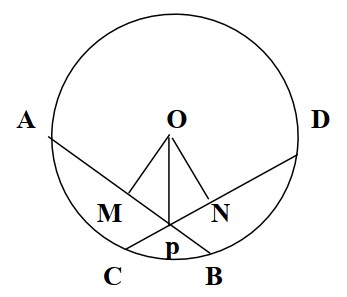
মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তে দুইটি সমান জ্যা AB ও CD পরস্পর P বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, PA=PD এবং PB=PC.
অঙ্কনঃ
কেন্দ্র O থেকে AB ও CD এর উপর যথাক্রমে OM এবং ON লম্ব আঁকি। O, P যোগ করি।
প্রমাণঃ
△MOP ও △NOP এর মধ্যে
∠OMP=∠ONP=900 [অঙ্কন অনুসারে]
OM=ON [সমান সমান জ্যা কেন্দ্র হতে সমদূরবর্তী]
OP সাধারণ বাহু।
∴ △MOP ≅ △NOP
∴ MP=NP……(i)
এখন
AB=CD [শর্ত মতে]
বা, ½AB= ½CD
বা, AM=DN [কেন্দ্র হতে অঙ্কিত লম্ব জ্যা কে সমদ্বিখন্ডিত করে]
বা, AM+MP=DN+MP [উভয়পক্ষে MP যোগ করি]
বা, AM+MP=DN+NP [(i) নং হতে]
বা, PA=PD…..(ii)
আবার,
AB=CD [শর্ত মতে]
বা, AB-PA=CD-PD [(ii) নং হতে]
বা, PB=PC
অতএব, PA=PD এবং PB=PC (প্রমাণিত)
২. প্রমাণ কর যে, বৃত্তের সমান জ্যা-এর মধ্যবিন্দুগুলো সমবৃত্ত।
সমাধানঃ
বিশেষ নির্বচনঃ
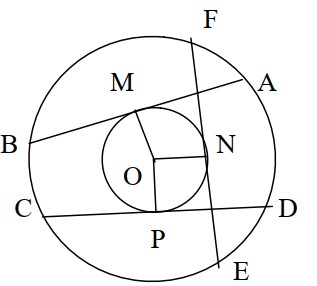
মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তে AB, CD ও EF তিনটি সমান জ্যা। AB, CD ও EF এর মধ্যবিন্দুগুলো যথাক্রমে M, P ও N। প্রমাণ করতে হবে যে, M, P ও N সমবৃত্ত।
অঙ্কনঃ
O, M; O, N এবং O, P যোগ করি।
প্রমাণঃ
আমরা জানি, কেন্দ্র হতে অঙ্কিত লম্ব জ্যা কে সমদ্বিখন্ডিত করে।
যেহেতু M, P, N যথাক্রমে জ্যা AB, CD, EF এর মধ্যবিন্দু সেহেতু OM, OP, ON যথাক্রমে AB, CD, EF এর উপর লম্ব।
তাহলে, OM, OP, ON ই কেন্দ্র হতে জ্যা তিনটির দূরত্ব।
এখন,
OM=OP=ON [বৃত্তের সকল সমান জ্যা কেন্দ্র হতে সমদূরবর্তী]
সুতরাং, O কে কেন্দ্র করে OM, ON, OP এর সমান ব্যাসার্ধ নিয়ে বৃত্ত আঁকলে তা M, N, P বিন্দু দিয়ে যবে।
অতএব, M, N, P সমবৃত্ত (প্রমাণিত)
৩. দেখাও যে, ব্যাসের দুই প্রান্ত থেকে এর বিপরীত দিকে দুইটি সমান্তরাল জ্যা অঙ্কন করলে এরা সমান্তরাল হয়।
সমাধানঃ
বিশেষ নির্বচনঃ
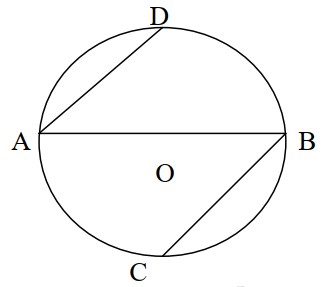
মনে করি, O কেন্দ্র বিশিষ্ট বৃত্তের AB ব্যাস। AB ব্যাসের A প্রান্ত থেকে AD জ্যা এবং B প্রান্ত থেকে BC জ্যা অঙ্কন করা হয়েছে। প্রমাণ করতে হবে যে, AD।।BC.
প্রমাণঃ
AD=BC [শর্তানুসারে]
AB তাদের ছেদক।
∴∠DAB=∠CBA
ছেদকের উভয় পাশের একান্তর কোণগুলো সমান হলে রেখাদ্বয় সমান্তরাল।
∴AD।।BC (প্রমাণিত)
৪. দেখাও যে, ব্যাসের দুই প্রান্ত থেকে এর বিপরীত দিকে দুইটি সমান্তরাল জ্যা আঁকলে এরা সমান হয়।
সমাধানঃ
বিশেষ নির্বচনঃ
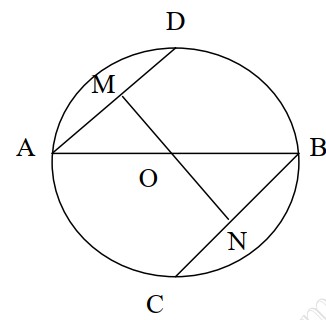
মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তে AB ব্যাস। AB এর A প্রান্ত থেকে AD জ্যা এবং B প্রান্ত থেকে BC জ্যা আঁকা হল এবং AD।।BC। প্রমাণ করতে হবে যে, AD=BC.
অঙ্কনঃ
কেন্দ্র O থেকে AD ও BC এর উপর যথাক্রমে OM ও ON লম্ব আঁকি।
প্রমাণঃ
△AOM ও △BON এর মধ্য,
∠OMA=∠ONB [OM⊥AD; ON⊥BC]
∠MAO=∠NBO [AD।।BC ও AB ছেদক]
AO=BO [একই বৃত্তের ব্যাসার্ধ]
∴ △AOM ≅ △BON
∴ OM=ON
তাহলে, AD=BC [বৃত্তের কেন্দ্র হতে সমদূরবর্তী সকল জ্যা সমান]
∴ AD=BC (প্রমাণিত)
৫. দেখাও যে, বৃত্তের দুইটি জ্যা-এর মধ্যে বৃহত্তর জ্যা টি ক্ষুদ্রতর জ্যা অপেক্ষা কেন্দ্রের নিকটতর।
সমাধানঃ
বিশেষ নির্বচনঃ
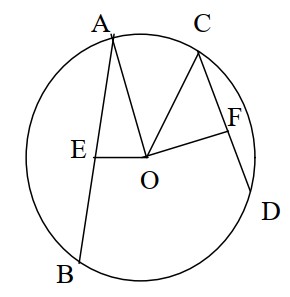
মনে করি, O কেন্দ্র বিশিষ্ট বৃত্তে AB ও CD দুইটি জ্যা এবং AB>CD। AB ও CD এর উপরে লম্বদ্বয় যথাক্রমে OE ও OF। দেখাতে হবে যে, OE<OF.
অঙ্কনঃ
O, A ও O, C যোগ করি।
প্রমাণঃ
যেহেতু, OE⊥AB এবং OF⊥CD
AE= ½AB, CF=½CD [বৃত্তের কেন্দ্র থেকে জ্যা এর উপর অঙ্কিত লম্ব জ্যাকে সমদ্বিখন্ডিত করে]
কিন্তু, AB>CD
∴AE>CF
এখন, △OAE এ OA2=AE2+OE2
এবং △OCF এ OC2=CF2+OF2
কিন্তু, OA=OC [একই বৃত্তের ব্যাসার্ধ]
∴ OA2=OC2
∴ AE2+OE2=CF2+OF2
এখন, AE>CF হওয়ায়
AE2>CF2
∴ OE2<OF2
বা, OE<OF
অর্থাৎ, বৃহত্তর জ্যাটি ক্ষুদ্রতর জ্যা অপেক্ষা কেন্দ্রের নিকটতর। (দেখানো হলো)
৬. O কেন্দ্র বিশিষ্ট বৃত্তে PQ এবং RS দুটি সমান জ্যা এর মধ্যবিন্দু যথাক্রমে M ও N।
ক) 314 বর্গ সেমি ক্ষেত্রফল বিশিষ্ট বৃত্তের ব্যাসার্ধ নির্ণয় কর।
সমাধানঃ
আমরা জানি,
বৃত্তের ক্ষেত্রফল= πr2 [r=ব্যাসার্ধ]
দেওয়া আছে, বৃত্তের ক্ষত্রফল=314 বর্গ সেমি।
প্রশ্নমতে,
πr2=314
বা, 3.1416*r2=314
বা, r2=314/3.1416
বা, r2=99.949
বা, r=√99.949
বা, r=9.997
∴বৃত্তের ব্যাসার্ধ=9.997 সেমি.
খ) প্রমাণ কর যে, OM=ON।
সমাধানঃ
বিশেষ নির্বচনঃ
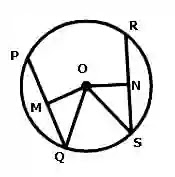
মনে করি, O কেন্দ্র বিশিষ্ট বৃত্তে PQ ও RS দুইটি সমান জ্যা যাদের মধ্যবিন্দু যথাক্রমে M ও N। প্রমাণ করতে হবে যে, OM=ON।
অঙ্কনঃ
O, Q ও O, S যোগ করি।
প্রমাণঃ
আমরা জানি, বৃত্তের কেন্দ্র থেকে অঙ্কিত লম্ব জ্যা কে সমদ্বিখন্ডিত করে।
O বৃত্তের কেন্দ্র, জ্যা PQ ও RS এর মধ্যবিন্দু M ও N।
তাহলে, OM⊥PQ এবং ON⊥RS…….(i)
এখন, △OMQ ও △ONS এর মধ্যে,
∠OMQ=∠ONS=এক সমকোণ [(i) নং হতে]
MQ=NS [যেহেতু PQ=RS, জ্যা PQ ও RS এর মধ্যবিন্দু M ও N ]
OQ=OS [একই বৃত্তের ব্যাসার্ধ]
∴ △OMQ ≅ △ONS
অতএব, OM=ON [প্রমাণিত]
গ) PQ এবং RS জ্যাদ্বয় বৃত্তের অভ্যন্তরে পরস্পরকে ছেদ করলে প্রমাণ কর যে, একটির অংশদ্বয় অপরটির অংশদ্বয়ের সমান।
সমাধানঃ
বিশেষ নির্বচনঃ
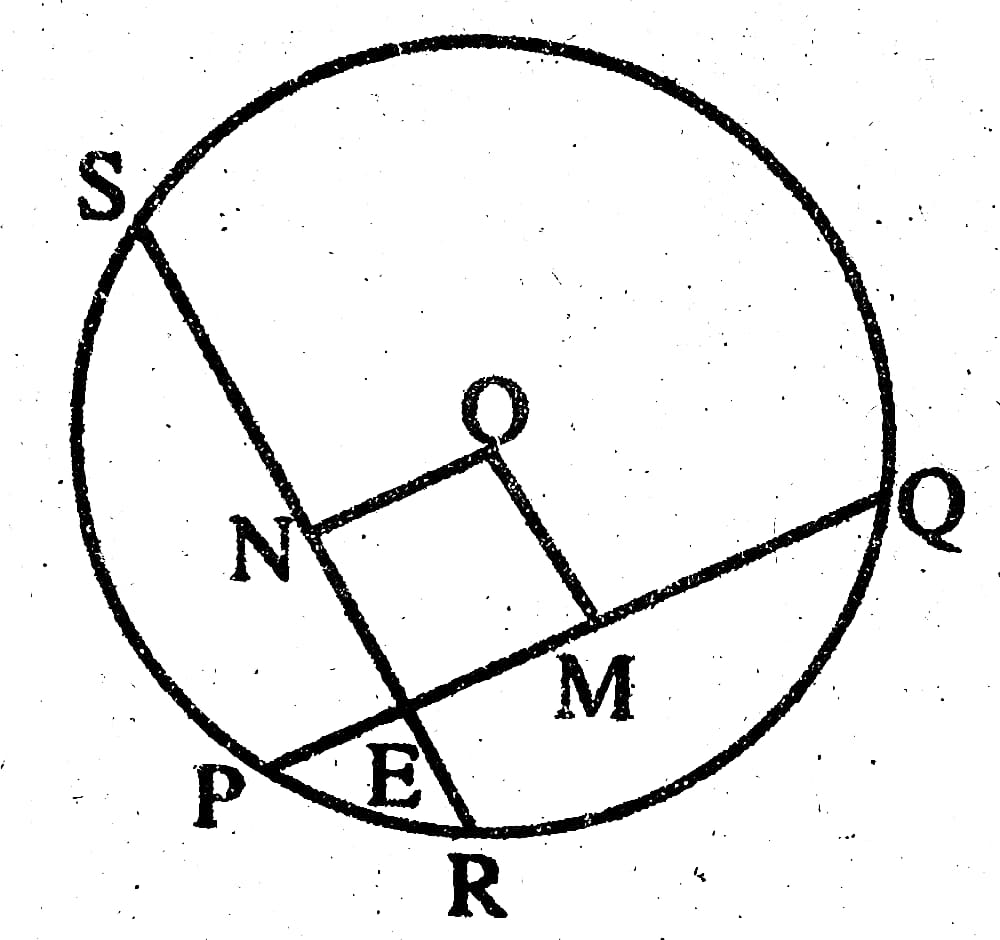
মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তে দুইটি সমান জ্যা PQ ও RS পরস্পর E বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, PE=RE এবং QE=SE.
অঙ্কনঃ
কেন্দ্র O থেকে PQ ও RS এর উপর যথাক্রমে OM এবং ON লম্ব আঁকি। O, E যোগ করি।
প্রমাণঃ
(১) বৃত্তের কেন্দ্র এবং OM⊥ জ্যা PQ.
∴ PM = QM
অর্থ্যাৎ PM = 1/2 PQ
আবার, ON ⊥ জ্যা RS.
অর্থ্যাৎ RN = 1/2 RS
(২) এখন, PQ = RS
বা, 1/2PQ = 1/2RS
বা, QM = SN
আবার, OM এবং ON, কেন্দ্র হতে PQ এবং RS জ্যাদ্বয়ের দুরত্ব।
| Class 8 math book all chapter solution Bangla version pdf | ৮ম শ্রেণি গণিত বই সম্পূর্ণ সমাধান PDF |
tags: Bangladesh, Bangla, Bengali, Class 8/jsc math solution 2021 pdf, 8th class maths guide pdf free download, math book solution BD, JSC srijonshil math, Chapter 10.2, বৃত্ত, বৃত্তের জ্যা


